In a parallelogram, prove that the ratio of any side to an altitude of adjacent side is same for all its sides.


  1. Home
  2. Math
  3. All Questions
Answer:


Step by Step Explanation:
  1. Let ABCD is a parallelogram as shown below. We have extended its sides to show the altitudes as CP and CQ.
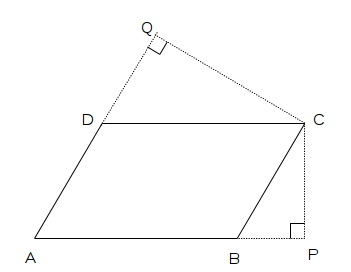
  2. Lets first consider side AB. Its adjacent sides are AD and BC. From the picture, we can see that altitude for AD and BC is CQ.
    Therefore the required ratio is,
     
    AB
    CQ
     
  3. Similarly, these ratios will be as following for other sides:
     
    CD
    CQ
     ,  
    AD
    CP
     ,  
    BC
    CP
     
  4. Therefore we need to prove that,
     
    AB
    CQ
      =  
    CD
    CQ
      =  
    AD
    CP
      =  
    BC
    CP
     
  5. If we compare triangles ΔBPC and ΔDQC, we observe following,
    - ∠DQC = ∠BPC ..... (Both are right-angle)
    - ∠DCQ = ∠BCP ..... (∠DCQ = 90° -∠BCD and ∠BCP = 90° -∠BCD)
  6. Since two angles are equal, triangles ΔBPC and ΔDQC are similar triangles.
  7. Since the ratio of corresponding sides of similar triangles is same,
     
    BC
    CP
      =  
    CD
    CQ
     
  8. Also since AB = CD and BC = AD,
     
    AB
    CQ
      =  
    CD
    CQ
      =  
    AD
    CP
      =  
    BC
    CP
     

You can reuse this answer
Creative Commons License